跳转至

0x14 trie(字典树)

[toc]

1. 什么是trie

trie是retrieval的短写，读作try。也叫做字典树，本质上就是一颗节点为数组的树，也可以理解为26叉树（对于存储单词来说）。tried解决的问题是信息的大量检索问题，设想我们存储了n个单词，需要多次检索。朴素算法下，对n个单词线性的搜索，时间复杂度为O(n)。而后我们可以对单词进行字典序排序，通过二分搜索，检索的时间复杂度降为了O(log n)。

我们可能会发现，对于单词来讲，构成单词的永远是26个字母，用字典序+二分可能还有优化的余地，能不能将开头为a的分到一类，b的一类，而后对单词中的每一位都这样分类，这样比对单词中的每一位，就能快速找到是否存了这个单词。这就是字典树，trie。最终的时间复杂度只和单词的长度有关系，因为单词大部分长度都是有限的且很短，可以将单词长度理解为一个很小的常数，这样trie检索的时间复杂度就是O(1)。

2. 为什么要用trie

trie用于多次查询的场景，是一种空间换时间的做法（trie中存在很大的空间冗余），但是其查询速度可以达到O(1)。因此对于一些对查询速度有要求、存储的内容可以编码为有限长度的信息来说，trie可以提供快速的查询。

3. trie的实现

3.1. 正常实现

trie的实现就是一棵树，每一层代表单词中的每一位，因为有26个单词，因此对于每个节点需要用一个长度为26的数组来存储信息，也就是一棵26叉树。

trie

1
2
3
4
5
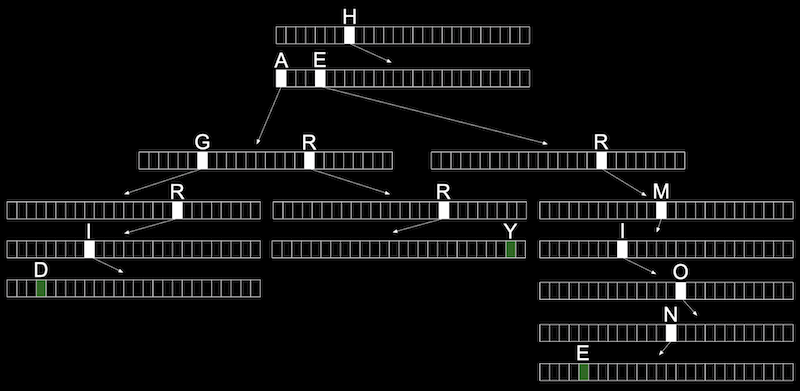
const int ALPHABET_SIZE = 26;
struct trie {
    trie *node[ALPHABET_SIZE];
    bool isEnd; // 用于区分结尾字幕和普通字母
}

trie需要执行的操作有两种，插入和查询。

对于插入来说，从根节点（单词的第一位）开始，如果该字母节点存在子节点指针，那么继续比对第二位，否则创建子节点。比对到最后一位时，代表单词的结尾，为了区分结尾字母和普通字母，我们需要给结尾字母节点一些额外信息。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
void insert(char *str, trie *t) {
    if (!str[0]) {
        t->isEnd = true;
        return;
    }
    int ci = str[0] - 'a';
    if (t->node[ci] == NULL) {
        t->node[ci] = new trie;
    }
    trie *p = t->node[ci];
    insert(str + 1, p);
}

对于查询来说，与插入类似，也是从根节点即单词的第一位开始比对，不同的是如果发现单词中某一位在trie中不存在，立刻返回不存在。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
bool query(char *str, trie *t) {
    if (!str[0]) {
        return t->isEnd;
    }
    int ci = str[0] - 'a';
    if (t->node[ci] == NULL) {
        return false;
    }
    trie *p = t->node[ci];
    return query(str + 1, p);
}

3.2. 优化

这里用的是动态分配的树，和链表一样，动态分配的树速度会慢，我们需要用数组模拟树。思路也和数组模拟链表一样，每个数组的元素用于模拟树的节点，对于节点有很多字段就用多个数组模拟。

1
2
3
4
5
6
7
8
const int ALPHABET_SIZE = 26;
const int N = 1e5 + 10;
// 假设最多需要1e5个trie节点
int trie[N][26];
int cnt[N];
int idx;
// 这里两个数组，对应着trie中的两个字段
// idx 用于记录分配节点的数量

插入和查询类似，因为算法题多为一个全局变量，因此就直接迭代做了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void insert(char *str) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int ci = str[i] - 'a';
        if (!trie[p][ci]) {
            trie[p][ci] = ++idx;
            // 分配一个新节点
        }
        p = trie[p][ci];
    }
    cnt[p]++;
    // 单词结束
}

int query(char *str) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int ci = str[i] - 'a';
        if (!trie[p][ci]) {
            return 0;
        }
        p = trie[p][ci];
    }
    return cnt[p];
}

3.3. 拓展

最大异或对

在给定的 N 个整数 A1，A2……AN 中选出两个进行 xor（异或）运算，得到的结果最大是多少？

1≤N≤1e5,

0≤Ai<2^31

输入样例：

3

1 2 3

输出：

3

首先思考，什么样的两个整数异或运算得到的结果最大。根据异或运算的定义，是对比每一个二进制位，如果相同为0，不同为1。因此所有二进制位都不同的两个整数异或运算结果最大，或者说，尽量保证高位的二进制值不同（高位1>低位1）。

那么问题就来到了，如何快速找出尽可能高位二进制不同的整数。要想找出最大的异或结果，那么就需要对每个整数都找出其能够得到的最大异或值，而后取最大值。最多有1e5个数字，因此本题最好能在线性时间解决。可以考虑用trie来解决。

将每个整数编码为32位二进制数，这样trie就变成了32层的二叉树，最多需要1e5 * 32 个节点（可以继续优化，根据树的性质）。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const int N = 1e5 * 32;
int trie[N][2];
int idx;

void insert(int v) {
    int p = 0;
    // 第0位是符号位，因为本题都是正数，因此可以无视
    for (int i = 30; i >= 0; i--) {
        int ri = (v >> i) & 1;
        // 由高至低取出每一位
        if (!trie[p][ri]) {
            trie[p][ri] = ++idx;
        }
        p = trie[p][ri];
    }
}

int query(int v) {
    int p = 0;
    int res = 0;
    for (int i = 30; i >= 0; i--) {
        int ri = (v >> i) & 1;
        ri = !ri;
        // 取出来是0那么要查的就是1，因此要取个负
        ri = trie[p][ri] ? ri : !ri;
        // 因为上层节点的存在，本层在0和1之间一定存在一个结果，尽量取需要的结果
        p = trie[p][ri];
        res |= ri << i;
        // 将该为赋值到结果上去
    }
    return res ^ v;
    // 把v的最大异或值返回
}
最后更新: February 13, 2023